Project Euler: Aufgabe 18

Diesen Beitrag habe ich ursprünglich für Daniel geschrieben, weil ich ihm meinen Lösungsweg für Aufgabe 18 von Project Euler erklären wollte. Nun, etwa zehn Minuten später, veröffentliche ich ihn auf meinem Blog.

Wir suchen die maximale Summe eines Pfades durch den Graphen. Der Pfad soll beim Wurzelknoten starten und von dort aus nach ganz unten führen. Bei diesem kleinen Graphen sieht das folgendermaßen aus:

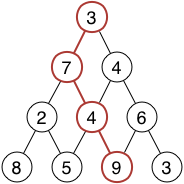
Der rot markierte Pfad ist der Pfad mit der maximalen Summe: 3 + 7 + 4 + 9 = 23

Nun ergänzen wir unseren Graphen um eine weitere Ebene von Knoten.

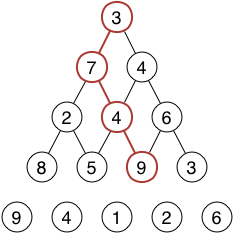
Um nun den Pfad mit der maximalen Summe zu finden, müssen wir nicht die Summen aller möglichen Pfade bis zu den Knoten in der untersten Ebene neu berechnen. Die Summe des rot markierten Pfads kennen wir schon, und wir können sie weiterverwenden, denn Teilpfade eines Pfades mit maximaler Summe zwischen zwei Knoten sind ebenfalls Pfade mit maximaler Summe (Das bedeutet nicht, dass der rote Pfad Teilpfad jedes maximalen Pfades von der Wurzel bis zur untersten Ebene ist!). Diese Beziehung veranschaulichen wir uns wie folgt:

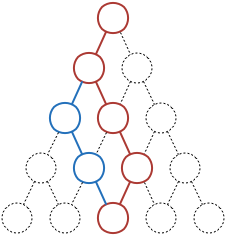
Sei der rote Pfad wieder der maximale Pfad vom Wurzelknoten bis zum dritten Knoten von links in der untersten Ebene (Knoten [5, 3]). Dann kann es keinen (hier blau markierten) Pfad geben, der eine größere Summe erzeugt als der rote Teilpfad daneben. Der Pfad, der von [2, 1] bis [5, 3] die größte Summe erzeugt, muss der rote Pfad sein, denn sonst wäre der rote Pfad vom Wurzelknoten bis [5, 3] nicht mehr der maximale Pfad (sondern der Pfad, der den blauen Teilpfad enthält; Beweis durch Widerspruch, as you do).

Weil wir nur an der maximalen Summe interessiert sind, merken wir uns nun keine Pfade mehr, sondern einfach für jeden Knoten die maximale Summe, die bis zu ihm erreicht werden kann. In unserem Graphen, den wir um eine Ebene ergänzt haben, sind das folgende Summen: (rechnet ruhig selbst nach!)

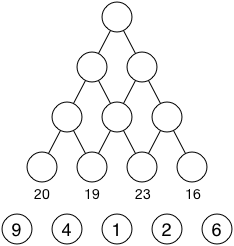
Um nun für die nächste Zeile die maximal erreichbaren Summen zu berechnen, müssen wir für jeden Knoten höchstens zwei Additionen durchführen (für die Knoten ganz links und rechts nur eine) und das größere Ergebnis speichern.

20 + 9 = 29, max(20 + 4, 19 + 4) = 24, …

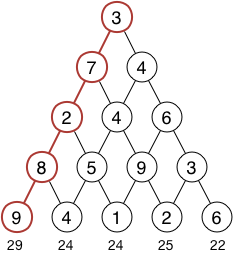
Die maximale Pfadsumme im ergänzten Graphen ist also 29.